Understanding Precession of the Equinox

EVIDENCE OUR SUN IS PART OF A LONG CYCLE BINARY STAR SYSTEM

 

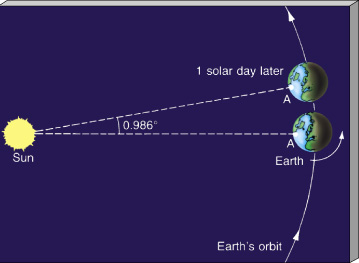
It all starts with the ILLUSION

Precession of the equinox is the observed phenomenon whereby the equinoctial point precesses (moves backward) through the constellations of the Zodiac at the rate of approximately 50.24 arc seconds annually.

In examining the mechanics of the motion of precession of the equinox, one will notice two observables:

1. The North Celestial Pole on its 23.45 degree incline slowly traces a large circle in the sky, pointing to different pole stars over thousands of years, and

2. The observer on Earth, at the point of equinox changes his orientation to inertial space at the current rate of about 50.24 arc seconds annually. At this rate the entire precession cycle time required to traverse all twelve constellations of the ancient Zodiac, is 25,792 years, although evidence indicates it is declining.

Some years ago it was observed that if the Earth’s axis did wobble due to lunisolar forces, it would slowly change the seasons within the calendar.

For example, in the northern hemisphere it would eventually become winter in the months of July and August, and summer in January and February. This is because the seasons are indirectly caused by axial tilt (i.e. summer when that hemisphere leans closer to Earth, winter when it leans away, etc.). Therefore, if the axis was tilted for any other reason, such as lunisolar wobble, it would cause seasonal shift.

Noticing that the seasons have not been changing (the equinox still falls at the same time in the calendar each year after adjusting for leap movements synching the Earth’s rotation with the calendar) lunisolar precession theory now requires that the equinoctial point itself must precess around the Earth’s orbital path around the Sun. This theoretical solution avoids the occurrence of seasonal shift that the original theory implied, but causes other problems because it implies the Earth does not complete a 360-degree motion around the Sun equinox to equinox.

To visualize the movement: if the Earth’s path around the Sun were made of 25,792 fixed positions, numbered 1 through 25,792, then in year one the vernal equinox would occur in position 25,791, the next year it would occur in position 25,790, the next year it would occur in position 25,789, the next year in position 25,788, etc. thereby slipping one position per year. At the end of 25,792 years, the vernal equinox would have regressed all the way around the Sun to finally occur once again at its original starting position.

Under lunisolar precession theory it is thought that the Sun and Moon’s gravitational influence acting upon the Earth’s bulge causes the Earth’s axial gyration that in turn results in the Earth’s changing orientation to inertial space, observed as precession of the equinox. The theorized annual axial tilt of about 50.24 arc seconds per year is thought to cause the equinox to occur slightly earlier in the Earth’s orbit path around the Sun, resulting in an orbit geometry of 359 degrees 59’ and 10” equinox to equinox. While this theoretical solution works mathematically and avoids the hypothetical problem of seasonal shift it does not agree with lunar cycles which indicate the Earth does indeed travel around the Sun 360 degrees (relative to the Sun) in an equinoctial year. This can be proved by carefully examining lunar cycle equations and eclipse predictions. Indeed, eclipses have been accurately predicted for many years, long before the latest nuances of lunisolar precession theory required the Earth to have a like equinox approximately 22,000 miles short of a complete revolution around the Sun.

All the way back in 1914, a scientist named Percival Lowell had this figured out.  He published the following paper in the Astronomical Journal.  This article shows how to calculate the Precession of Mars and indicates there are two Precessions summed together to get the total precession.  Approximately 50.24 arcseconds is attributed to the General Precession which is the precession of the Sun and solar system.  The other is luniprecession which accounts for 0.11 arcseconds, about 1/500th, of the effects of General Precession. Read this 1914 publication for detail and ask yourself this question.  WHY HAS THIS BEEN BURIED IN NASA ARCHIVES and not used to determine the truth?

http://adsabs.harvard.edu/full/1914AJ…..28..169L

It should be noted that even though the Earth travels 360 degrees around the Sun, relative to the Sun, measured equinox to equinox, this motion only equates to 359 degrees 59’ 10” relative to the fixed stars (distant quasars). The only way the Earth (and the accompanying Moon) could travel 360 degrees around the Sun, yet show a lesser motion relative to the fixed stars, is if the entire solar system itself moved in a curved elliptical pattern through space.

The principal cause of precession then is not an Earth that wobbles relative to the Sun, but a solar system that moves in a curved elliptical pattern through space resulting in all the current observables of precession; a changing pole star and movement of the equinoctial point through the zodiac, but the wobble is only apparent relative to the fixed stars because it does not exist relative to the Sun.

The gist of this paper is a new model that more simply explains precession and current solar system mechanics.

In the new model, our Sun “moves through a curved pattern” through space as it orbits the Milky Way Galaxy. This causes an “apparent wobble” to the observer on Earth which is an illusion created by the solar systems curved movement through space; thus producing an observable “precession of the equinox” without creating any season shifting issues and cause another riddle in for the old lunisolar theory.

We remove the riddle without requiring any movement of the equinoctial points on the Earth’s orbital path, or new interpretations of equinoctial years, thereby allowing the equinoctial year to which we adjust UTC (Coordinated Universal Time) to reflect a 360 degree motion of the earth around the Sun, but not through space.  The motion through space as viewed from a distant star would indicate the Earth moves in a cork screw pattern around the Milky Way in a fight for momentum with its binary companion.    This cork screw pattern creates the Illusion of the Precession of the Equinox as understood by the old lunisolar theory and is evidence that the 50.24 acrseconds of precession is not a wobble, but an illusion.

NEW MODEL CONFIGURATION

According to Newtonian physics the only force that could cause the Sun to display such a curve would be another large mass to which the Sun is gravitationally bound, which is by definition a binary star system. In this model, the Copernican Third Motion of the Earth would be caused primarily by the Sun’s curved path in a binary orbit, rather than strictly lunisolar forces.

Visually, the new model is one of a rotating object (the Earth) in an almost circular orbit around a second object (the Sun), which in turn is an elliptical orbit around a third object (the binary center of mass of the Sun and its companion star). If the Earth’s orbit and the Sun’s orbit are relatively fixed (i.e. given) then the equations of classical mechanics predict that the axis of rotation of the first rotating object (the Earth) will precess (relative to inertial space) at a rate dictated by the Sun’s path around its binary center of mass. To an observer on Earth the first objects axis will “appear” to precess by 360 degrees, in the same amount of time it takes the second object to undergo a complete orbit around the third object, independent of the masses and distances involved. In this model the Earth’s axis does not really wobble, or change relative to the Sun, but it produces the same “observable” now attributed to lunisolar precession: a precession of the equinox. From this we conclude:

Acceleration (and eventual deceleration) of the rate of precession will depend on the eccentricity of the binary orbit. From Kepler’s Third Law, we know that all orbits are elliptical and objects leaving apoapsis accelerate to periapsis and then decelerate leaving periapsis. Consequently, we now have an explanation for why the precession rate is now accelerating, and we also have a logical reason for why the rate cannot be extrapolated ad infinitum. Indeed, the most significant clue that precession represents a binary orbit is it’s universally recognized but until now, unexplained acceleration.

Depending on what part of the orbit the observer is on, if he assumes that he is in a circular orbit because it takes a couple of centuries for the acceleration to really become apparent, then he will over/underestimate the orbit period. The precession cycle, now estimated at 25,792 years has been continually reduced over the last several hundred years. According to our calculations, based on an elliptical orbit it is expected to average 24,000 years for a complete cycle (orbit).

To summarize: the annual precession rate is accelerating. However it is not the “wobble” rate increasing, it is the rate of orbit around our barycenter, as our Sun leaves apoapsis. Also, one cannot simply extrapolate the current rate to get the orbit period. Elliptical orbit equations are key to understanding precession. In the current model, there is not a good explanation for resolution of periodicity. Periodicity is a key tenet of the Milankovitch Cycle. (Berger 1977)

Beyond explaining why precession now seems to accelerate, a binary star model appears to better explain other observed phenomena. For example: it would explain the unusual distribution of angular momentum, a fact that has long perplexed scientists developing solar system formation theories. (Caroll and Ostlie 1996)

In a binary model the Sun’s angular momentum is in its movement through space, not just in it’s spin axis.  A binary model might also help explain the non-random path of certain long-cycle comets (Svitil October 2001), without requiring the existence of a tenth planet or huge quantities of dark matter within the solar system. Also, the recent finding that our solar system has a sheer edge (Allen et al. 2001) is now readily explainable, indeed expected in a binary system.  Another new finding that was published in 2010 is that the Voyager spacecraft trajectories are behaving as if they are being acted upon by an unknown force as they leave the grip of the sun and feel the grip of our sun’s companion.

Furthermore, the efficacy of the Earth’s changing orientation to inertial space, being a byproduct of the Suns orbit around its companion star, rather than solely a specific gravitational effect upon one part of the Earth’s mass, fits well with a solar system designed for maximum economy.

Based on this work to date, the following statements are consistent with observed data:

Our Sun is probably part of a binary system, gravitationally bound to another star, likely a dark companion, which is estimated to be 1000 to 4,000 A.U. distant (0.0155LY to 0.062 LY). We are open to other possibilities such as a visible star, however, because this would require a different understanding of long range gravitational effects (i.e. MOND or other new theories). We are not going to speculate on the full range of potential companion stars.

The Sun’s path currently curves at about 50.24 arc seconds per year (one degree every 71.657 years) around its apparent binary center of mass, and the Sun is now accelerating, at the approximate rate of 0.000349 (arc seconds per year) per year.  The old lunisolar model fails to explain this acceleration.  The binary theory explains the acceleration as movement from apoapsis (at farthest orbit) to periapsis (at closest orbit).   At the closest orbit, the precession accelerations zero and as the companion stars pass periapsis, precession will begin to decrease.

This change in acceleration also affects General Relativity which can be noted also to be the possible discrepancies in relativity calculations.

The apparent binary orbit plane is expected to be the same as, or within a few degrees of, the invariable plane (the angular momentum plane of the solar system).

The Earth’s changing orientation to inertial space (as required by any binary orbit of our Sun), can be seen as Precession of the Equinox. This fact has been masked by the illusion called the lunisolar explanation for precession.

The current apparent binary orbit speed is one cycle every 25,792 years, but due to acceleration (as we move away from apoapsis), is expected to average approximately 24,000 years per complete orbit.

Models based on Kepler’s Law for elliptical orbits appear to predict the changing precession rate better than current wobble theory.

The third motion of the Earth (wobble) does exist as an observable phenomenon, but not as axial movement relative to the Sun. Independent axial movement is probably limited to nutational nodding and Chandler wobble and is negligible (!/5ooth) when compared to precession.

Occam’s Razor requires consideration of the binary star concept unless physical evidence is available that is clearly inconsistent with the model. We are not aware of such evidence.

Further arguments in support of a binary model are summarized below:

NEW MODEL PRODUCES SAME PRECESSION OBSERVABLE WITHOUT COMPLEXITY

Early lunisolar wobble required the pole to move by about one degree every 71.5 years based on the current precession rate, hence the pole should have moved about 6 degrees since the Gregorian Calendar change (420 years ago), thereby causing the equinox to drift about 5.9 days. This has not happened; the equinox is stable in time after making leap adjustments.

Therefore, it was theorized that the equinox must slip about 50 arc seconds per year along the ecliptic and the equinoctial year is only 359 degrees 59’ and 10” not 360 degrees. Although this solves the seasonal slippage issue it does not agree with lunar cycle data.

Astronomers sometimes use a 360-degree geometry to describe the Earth’s motion around the Sun, and they sometimes use 359 degree 59’ and 10”. Obviously the 360 degree motion in an equinoctial year works for calculating the moons position, eclipses, Saro’s cycles and the like but the lunisolar model of 359 degrees 59’ 10” in an equinoctial year works best for calculating the position of stars, quasars, and other extra solar system phenomena. In other words the lunisolar model works fine relative to the fixed stars but the other works well for purposes where the position of the fixed stars do not matter. Although both are useful for various calculation purposes, we assume there is still only one physical reality (at least if we exclude parallel universes) and therefore only one geometry is correct.

We can see that relative to the fixed stars the period from like equinox to like equinox occurs about 50” short of a 360 alignment with the same stars. In the current lunisolar paradigm, the wobbling axis supposedly causes this motion and it does work theoretically if you ignore the moons required motion in an equinoctial year. But the only system where both the moon data model can be correct (Earth around Sun 360 degrees in equinoctial year) and the Earth can appear to come up 50 arc seconds short of a 360 degree motion around the Sun (relative to the stars) in an equinoctial year, is one in which the entire solar system is curving through space at the rate of about 50 arc seconds per year. In this manner the Moon can travel with the Earth, the Earth and Moon and Sun can keep the integrity of their mathematical relationships, and the Earth can still appear to precess relative to the fixed stars with a wobble.

Now obviously the lunisolar model does not say the solar system is curving through space at 50 arc seconds per year. And yet there is no article or paper that addresses the subject. It is possible that those scientists that calculate eclipses, Saro’s cycles and other lunar cycle equations are not aware of all the subtle requirements of lunisolar precession theory- and that precession theorists do not concern themselves with moon cycle equations. Perhaps this paper will cause the subject to be examined and addressed.

Further to the point, if one assumes the cause of the equinoctial point slipping backward around the Earth’s orbit path at a rate of 50.29 arc seconds per year is due simply to the Earth wobbling at this exact same rate, then one must look deeper and realize that this implies the barycenter of the Earth stay the same with each 360 degree motion of the Earth around the Sun, and the reason the equinox happens earlier and earlier is because the Earth’s axial shift has caused the equinoctial position to appear earlier and earlier. However, this would mean the center of the Earth travels exactly 360 degrees, or once around the Sun each equinoctial year. Because the equinoctial year is now presumed to be less than 360 degrees (by the amount of precession) and only the sidereal year is presumed to represent a complete 360 degree motion of the Earth around the Sun (supposedly this is why we line up with the same stars in a sidereal year) then the barycenter to barycenter motion of the sidereal year would have to be more than 360 degrees, thereby showing the solar system is curving through space. If the slippage is not due solely to precession then why is the time delta between an equinoctial year and sidereal year attributed to precession, and why does the barycenter of the Earth slip at the same rate as precession?

One possible objection to this “Binary Model” is that the Earth and other planets of the solar system are not thought to change orientation to inertial space (the observable of precession) just because the solar system curves through space.

In reading Newton’s laws we can find nothing that would indicate the Earth would be unaffected by the Suns acceleration around a binary center of mass unless the Earth were perfectly spherical (both models agree it is not). Therefore it must be affected. We hear the opposite concern just as often. That is; if a companion star causes our solar system to slowly change orientation to inertial space it would cause all the planets to precess at the exact same rate as the earth. This seems highly unlikely given the fact that all the planets are subject to a multitude of varying forces such as different distances from the sun, different spin rates, different moon influences, etc. consequently the planets cannot all be expected to act exactly the same, for to do so would require them to escape all local influences. Remember gravity from the companion star and the resultant binary motion may be one factor that moves all masses in the solar system but it would not and could not affect all masses equally by overriding all local effects.

This is why there are several components to precession that must be summed to obtain the precession of each planet.  The rotation of the planet can contribute to precession.  The orbit of each moon can contribute a component of precession.  However, these planetary and lunar precessions are very small when compared to the General Precession (precession of the solar system).

In summary, a simple way to produce all the same observables as lunisolar precession theory; a precessing equinox and changing pole star, without any motions that are unexplained by classical mechanics, is a Sun curving through space in a binary system. In this model, planets gravitationally bound to stars curving through space, will experience a changing orientation to inertial space, commensurate with the stars rate of motion, unless offset or exaggerated by other local forces.

Sidereal vs. Solar Time Delta Rationale

If the delta between a sidereal “day” and a solar “day” is compensation for the curvature of an orbit (per textbooks), so too is the delta of a sidereal “year” vs. a solar “year” compensation for an orbit. The former is the orbit of the Earth around the Sun, the latter, the Sun around it’s apparent binary center of mass. Furthermore, just as the Earth’s delta between a sidereal “day” and a solar “day”, times the orbit period, (4 min X 365 = 1 day) is equivalent to the daily rate of change around it’s orbital center of mass (the Sun), so too should the Earth’s delta, between a sidereal “year” and a solar “year”, times X orbit period be equal to the annual rate of change around its apparent binary center of mass. (X = 25,770 years: the current rate of orbit around the postulated binary center of mass, 20 min X 25,770 years = 1 year) (minutes rounded produces 98% approximation).

Just because there is no known orbit that needs be compensated for by an annual delta between a sidereal year and a solar year, does not mean the 20 minute delta must be caused by something other than an orbit.

The burden of proof lies with those who support the current lunisolar precession theory which requires a different explanation for the two deltas.

Precession Calculation and Trend Rationale

A review of the scientific literature indicates that the annual rate of precession has been accelerating. (Fig. 1) The most reliable calculations that have been produced by Newcomb, Williams, etc., show a historical trend towards increasing annual precession rates (which implies a post apoapsis shrinking orbit period). We have found that Kepler’s orbital elliptical equations for a dual star model produce a more precise calculation of the change of precession and lend strong evidence to the argument that precession of the equinox is more adequately accounted for by an elliptical orbit rather than lunisolar forces. Indeed, if precession were primarily caused by the Sun and Moon tugging on the Earth’s equatorial bulge, the annual rate should not be constantly increasing, nor should orbit equations prove to be a better predictor of precession rates. Over the years other forces have been added to the lunisolar precession calculation including, other planets, tidal effects, movement of the Earth’s core, passing asteroids, etc.

According to the current single sun model, there is no reason for precession to ever change its increasing trend – a spinning top only slows down, there is no reason for it to speed up unless new force is applied. So in the past, precession (under the current model) must have been much smaller than it is now, and in the future, it will continue to increase. This historical extrapolation does not conform to the Milankovitch Cycle.

Given the fact a binary, elliptical orbit model provides the most efficient method for causing precession and predicting precession, then such a model should be considered the simplest descriptor of local celestial mechanics.

Modeling Assumptions

The issues discussed heretofore suggest the appropriateness of modeling binary systems to explore whether or not a binary star hypothesis is consistent with observed data. While an infinite number of potential binary system configurations are available for analysis, we narrowed the range by making three assumptions:

1. The orbital period for the Sun around the gravitational center of the binary system would be approximately 24,000 years (rounding from the currently calculated precession cycle of 25,792 years), if it were a circular orbit.

2. The actual orbital period will be greater or lesser than 24,000 years if the Sun’s orbit is non-circular, which is most likely. The degree to which the actual orbit is greater or lesser than the currently perceived period depends upon the eccentricity and the position of the Sun on that orbit relative to apoapsis or periapsis (this is because the Sun would be accelerating as it departs from apoapsis and decelerating as it departs from periapsis). Thus, if the Sun is closer to departing from apoapsis, the actual orbital cycle would be less than approximately 26,000 years, since that figure would have been derived from observation during the Sun’s slowest passage along its orbital path.

3. Because the calculated change in the precession cycle has increased by 0.034” over the last century, the Sun and solar system were assumed to be increasing in speed as the Sun accelerates away from apoapsis. So the annual increase in precession is attributed primarily to the increasing angular velocity of the Sun’s elliptical orbit around its binary companion.

With these assumptions, we tested orbital parameters at 1000 year intervals ranging from 24,000 years to 28,000 years, and for each orbital period, tested for assumed apoapsis at 500- year intervals into the past from 2000 A.D.

We found a very close fit between observed data and the orbital model assuming an orbital period of 24,000 years and with apoapsis around 2010 to 2014.

Revised Precession Calculations, New Constant, Future Estimates

Using the current Constant of Precession of 50.24”/y, the calculated period of revolution comes to 25,792 years. Calculating the annual change in precession of an orbit that has a period of revolution of 24,000 years, and at a point in 2012 as it passes periapsis, that has an angular velocity of 50.24 arc sec per year, returns an eccentricity of about 0.038.

If we are moving away from apoapsis as proposed, our orbital velocity should be increasing – we are speeding up with respect to the binary center of mass – which means that the period of revolution perceived over astronomically short periods of time is decreasing; this in turn requires the constant of precession to increase as time goes by. Currently the yearly change is about 0.000349”/y, but that will continue to increase for a few more years, until the Sun reaches periapsis. In terms of the calculated period of revolution, that corresponds to a yearly decrease of .178 years, ignoring the short cyclic influences of nutation, etc. This roughly corresponds with the changes in precession calculations that have been reported in the literature.

Therefore, we make the following estimates for the years 2011:

Year Precession

Period of Revolution (years)

2010 50.24”/y

25,792.035

2100 50.325866”/y

25792.164

In 1900, Simon Newcomb offered a formula for precession: 50.2564” + 0.000222 * (year – 1900) (U.S. Naval Observatory 1900)

We offer the following alternative formula based on the proposed binary system model: 50.245223” – 0.000349 * (2012- year)

Observed precession has changed by 0.0337 from 1900 to 2000, for a yearly change of 0.000337” . This precession delta is approximately ten times closer to our proposed annual precession of 0.000349” than Newcomb’s annual precession adjustment of 0.000222”.

Minimum precession is about 1 degree every 84 years when the Sun is at apoapsis, and the maximum precession is about one degree every 71.665 years when the Sun is near periapsis. The Earth will average about one degree of precession per 77.83 years over the 24,000 year cycle.

Dual Star Distance Calculation

In any binary system, the celestial bodies revolve around each other. More precisely, both stars orbit around a Center of Mass between them that corresponds to one of two focal points in each orbit (focus). In our proposed Dual Star Model, our Sun and its so-far unidentified companion rotate around each other every 24,000 years, and thus around their combined Center of Mass every 24,000 years.

Thus Kepler’s law for circular orbits for the proposed system:

N2 *D3 = G*(Massof Sun + Massof DualStar) Where: N = 2p / T

G = T =

D = MSUN

Gravitational Constant = 6.672 * 10-11 m3 kg-1 sec-2

Period of Revolution in seconds: sec Average distance between Sun and Dual Star in meters: m

= 1.9891 * 1030 kg

So: D3 * 4 p2 / (24,000 years)2 = G * (MSUN + MDUAL STAR )

For example, a Mass Dual Star = 0.08 of the Mass of the Sun (a dwarf):

D =  0.01344 L.Y. or 854 A.U.

D at 6 times the Mass of the Sun: 0.02384 L.Y. or 1514.6 A.U.

Comparing a binary model of our solar system versus a single sun model with lunisolar tugging at the Earth’s oblateness brings the following observations to light:

1. Majority of star systems are binary star systems(Richichi and Leinert 2000).  Why should we assume our solar system is not and we are the odd solar system .  Logic tells us that most likely, our solar system is like most others and is a binary system. 

2. Curved path of Sun through space simply explains the Earth’s changing orientation to inertial space, is an expected phenomena, and erases the illusion of a wobbling Earth.

3. Sidereal and solar year delta are a natural result of the binary orbit model.   The measured delta, as 50.24 arcseconds or 0.01395556 degrees, translates to the amount of orbit completed by our solar system around the barycenter of a binary system in a given year.  Divide 360 degrees by 0.01395556 and the period of binary orbit is found as 25,796.17834 years.

If the delta between a sidereal “day” and a solar “day” is compensation for the curvature of an orbit (per textbooks), so too is the delta of a sidereal “year” vs. a solar “year” compensation for an orbit. The former is the orbit of the Earth around the Sun, the latter, the Sun around it’s apparent binary center of mass (barycenter).

Furthermore, just as the Earth’s delta between a sidereal “day” and a solar “day”, times the orbit period, (4 min X 365 = 1 day) is equivalent to the daily rate of change around it’s orbital center of mass (the Sun), so too should the Earth’s delta, between a sidereal “year” and a solar “year”, times X orbit period be equal to the annual rate of change around its apparent binary center of mass. (X = 25,796 years: the current rate of orbit around the postulated barycenter of 0.1395556 degrees (25,796 years = 1 year) (rounded produces 99% approximation).

Just because there is no known orbit that needs be compensated for by an annual delta between a sidereal year and a solar year, does not mean the delta must be caused by something other than an orbit.

The burden of proof lies with those who support the current lunisolar precession theory which requires a different explanation for the two deltas.  However, in absence of proof of the old theory, I offer this document as proof our solar system is a binary solar system.

 

4. Angular momentum balances with dual star in a binary star system accounting for the missing momentum of the Sun.

5. Sheer edge of solar system as discovered in 2010 is not expected in the old lunisolar theory, however, a sheer edge is part of the binary model since mass is separated between companion stars.

6. Precession accelerates past apoapsis which fits the binary model.

7. Precession conforms to elliptical equation model and not a earth wobble model.

8. Curved Sun path allows observed wobble without causing rotational time problems, or requiring equinoctial slippage

9. Some long cycle comet paths should be channeled by dual mass which accounts for non random comets in our solar system.

10. No significant curvature in Sun’s path, requires Earth’s changing orientation to inertial space to be explained by complex theories that are still unproven; Occam’s Razor applies.

12. The Sidereal and solar year delta explanation conflicts with sidereal and solar day explanations.

13.  Distribution of angular momentum among planets still unexplained with old model while the binary model explains the distribution of angular moment.

14. Lunisolar precession should be constant (unless gravity of Sun and Moon are steadily increasing) but in fact precession calculations are continually altered

15. Old theory Precession should be relatively constant but it is not.   The binary model explains the increase and decrease in Precession.

16. The old theory rotational wobble creates time paradox that requires unexplained concurrent motions.

17. Comet paths should be random, but they are not (Murray 1999)

18. Voyager spacecraft’s trajectory is off (influenced by companion star).

CONCLUSIONS

Our solar system is part of a binary solar system and the precession of the equinox is an illusion caused by the movement of our solar system in a cork screwing elliptical pattern around the Milky Way Galaxy.

What awaits us at periapsis?

The angular momentum distribution of our solar system is a problem that has frustrated attempts at developing a reasonable theory of how the solar system developed. This problem disappears using a binary relationship model.

The gravitational effect of a binary companion could easily cause a non-random distribution of long-range comets. In a single sun system, an abrupt edge like the one just beyond our Kuiper Belt would not be expected. In a binary system a sheer edge would be normal and expected.

The current model of precession (spinning top slowing down) would mean a very different value of precession 100,000 years ago. In a binary relationship model, precession 100,000 years ago would be about the same as today –because it would be cyclical. This is in keeping with the accepted Milankovitch (Precession) Cycle. (Berger 1977)

Moreover, the binary model is a simpler more logical model for explaining the mechanics of our solar system and the motions of the Earth.

For example, unlike lunisolar theory the new model does not require concurrent slippage of the equinoctial point in order make precession work:

An equinoctial year, tropical year and solar year all, once again, represent a 360 degree motion of the Earth around the Sun.

The equinox occurs at the same place in the Earth’s orbit path each year (relative to the Sun). The ecliptic plane and celestial equator are once again fixed at the point of the equinox.

The calendar year, once again, represents a complete orbit of the Earth around the Sun. (Except for the differential between 365.25 (average days in a year) and 365.2422 (actual rotations in a year) that exists because mans calendar is made of whole days).

Also, the new model does not require extremely complex equations to predict precession. Nor do the new equations suffer a high degree of degradation over time:

The Earth’s changing orientation to inertial space is only minimally affected by the planets, tides, geo-physical movements, asteroids, etc. The principal source of movement is caused by the binary motion and the Sun curving through space, slowly changing the Earth’s orientation.

Precession can be more accurately, and easily predicted by plotting the angular velocity of the Sun in its binary orbit, and using this as the main input in precession calculations. The Sun’s angular momentum is now proportional to its mass, along with the other planets.

Precession’s annual increase is attributed primarily to the increasing angular velocity (curved motion) of the Sun’s “elliptical” orbit around it’s binary.

Precession waxes and wanes with the elliptical orbit of our Sun around its binary center of mass. In this model precession is cyclical and the current accelerating precession trend, expected in elliptical orbit, is now understandable.

Precession was never so small as to not exist and it will never become so large that we all wobble off the Earth. Minimum precession is about one degree every 72 years when the Sun is at apoapsis, and maximum precession is about one degree every 60 years when the Sun is near periapsis. The Earth will average about one degree of precession per 66.6 years over the 24,000 year cycle.

The new model does not require one cause to be given to explain the difference between a solar and sidereal “day” (orbital curvature) and another completely different principal to be given to explain the difference between a solar and sidereal “year”:

The sidereal year is 360 degrees plus precession due to the Sun’s motion

The sidereal year realigns with the same stars of a year ago, 20 minutes later than an equinoctial year (50.24 arc seconds), only because the solar system has curved through space by 50.24 arc seconds, along it’s binary orbit.

Just like the delta between a sidereal day and a solar day, the delta between a sidereal year and solar year is also due to curvature of an orbit. The “day” delta is due to curvature of the Earth around the Sun. The “year” delta is due to curvature of the Sun around its binary center of mass.

Many others are on board with the binary theory.  These scientists show a number of equations showing that theoretical lunisolar effects do not correspond with the Earth’s actual rotations, the other is a paper by the Italian scientist, Carlo Santagata, who has written an extensive treatise on where Newton and his successors miscalculated certain inputs of the lunisolar precession equations. Our role is not to confirm or deny the workings of lunisolar theory but rather to put forth a new model that solves current solar system enigmas in a simplified manner.

The binary model is a simpler, more logical model for explaining the mechanics of our solar system and the motions of the Earth.